Meta分析也是近两年的一个热点，漏斗图（Funnel plot）在文献中也很常见，其原理是基于研究效应的精确度与样本量呈正相关，即较小样本量的研究，通常分散的图形底部很宽的范围内，随着样本量的增大，精确度提高，研究的结果则集中在图形上部一个较窄的范围内。漏斗图若两边对称则无明显发表偏倚，两边不对称则可能存在发表偏倚，漏斗图只能提醒是否有偏倚存在，不能提供解决研究问题偏倚的方法，同时对称的漏斗图也不一定是不存在偏倚的，只有提高meta分析的质量和严谨的设计才是避免偏倚的最佳方式。

无意间看到在2013年左右发表的一篇文章介绍了如何绘制漏斗图，和大家分享：


# 需要安装meta包
library(meta)
# http://www.jebm.cn/article/2013/1671-5144-13-5-307.html
# 演示数据采用论文中数据
# 其中“sutdy”表示研究名称,“early.event”、“early.total”、“late.event”、“late.total”分别表示每个研究中早期和晚期应用糖蛋白Ⅱb/Ⅲa抑制剂治疗心肌梗塞溶栓出现事件的人数及研究总人数
study <-
  c(
    "RELAx-AMI 2007",
    "ERAMI 2006",
    "REOMOBILE 2004",
    "Rakouski 2007",
    "Reopro-BRIDGING 2004",
    "Zomorman 2002",
    "Emre 2006",
    "Cutlip 2003",
    "On-TIME 2004",
    "INTAMI 2005",
    "On-TIME 2006"
  )

early.event <- c(25, 7, 11, 8, 8, 9, 10, 7, 46, 18, 41)
early.total <- c(105, 40, 48, 25, 28, 56, 32, 23, 243, 53, 171)
late.event <- c(11, 5, 8, 3, 2, 1, 4, 6, 36, 5, 27)
late.total <- c(105, 40, 52, 30, 27, 56, 35, 30, 244, 49, 142)
mydata <-
  data.frame(study, early.event, early.total, late.event, late.total)
names(mydata) <-
  c("sutdy",
    "early.event",
    "early.total",
    "late.event",
    "late.total")

# 计算各种影响因素
mymeta <-
  metabin(
    early.event,
    early.total,
    late.event,
    late.total,
    data = mydata,
    studlab = study,
    comb.random = TRUE,
    # sm 可以选择的方法，这里涉及很多meta分析的名词就不一一解释了
    #
    # Risk ratio (sm = "RR")，又称相对危险度RR（Relative Risk）（也称为风险比）是前
    # 瞻性研究（队列研究）中常用的指标，它是暴露组的发病率与非暴露组的发病率之比，
    # 用于说明前者是后者的多少倍，是用来表示暴露与疾病联系强度的指标
    #
    # Odds ratio (sm = "OR")，优势比，指病例组中暴露人数与非暴露人数的比值除以对照组中暴露
    # 人数与非暴露人数的比值
    # Risk difference (sm = "RD")，风险差异
    # Arcsine difference (sm = "ASD")
    # Diagnostic Odds ratio (sm = "DOR")
    sm = "OR",
    method = "I"
  )
# 采用“Harbord”法进行漏斗图的不对称检验, P=0.011 84,说明漏斗图存在明显不对称，存在偏倚
metabias(mymeta)

# 对缺失进行剪补
mytrimfill <- trimfill(mymeta)
# 绘制漏斗图
funnel(
  mytrimfill,
  comb.fixed = TRUE,
  xlab = "Odds ratio",
  comb.random = TRUE,
  level = 0.95,
  contour = c(0.9, 0.95, 0.99),
  col.contour = c("darkgreen", "green", "lightgreen")
)
legend(
  4.2,
  0.05,
  c("0.1 > p > 0.05", "0.05 > p > 0.01", "< 0.01"),
  fill = c("darkgreen", "green", "lightgreen")
)

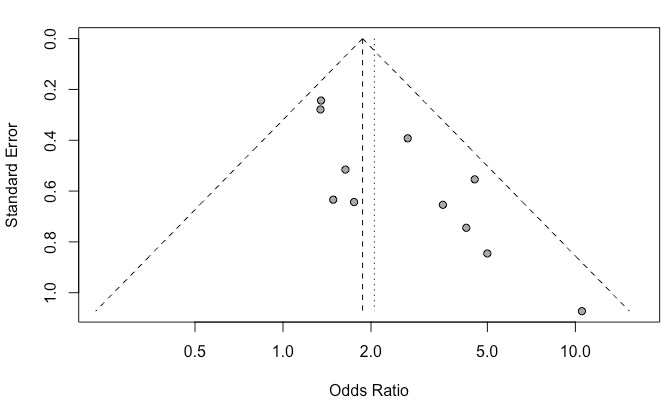
未经过剪补的漏斗图（代码未给出，可以结合上面去掉trimfill，直接用mymeta即可得到）

剪补后的附加轮廓线漏斗图如下：

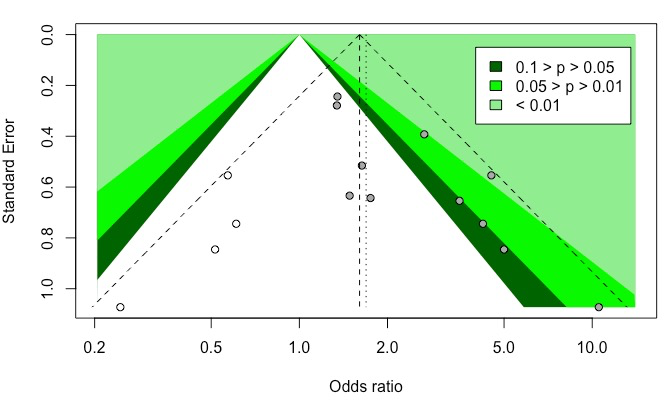
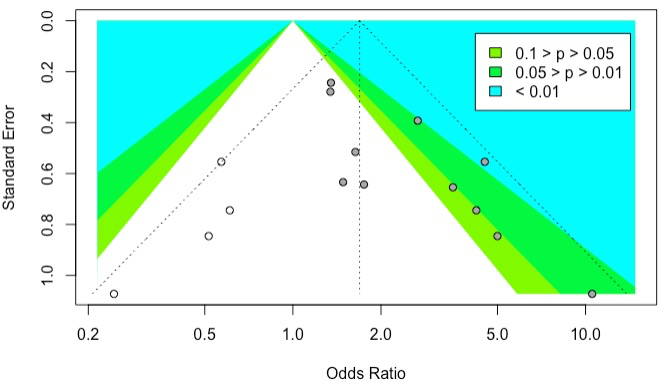
结合原始图和剪补后的附加轮廓线漏斗图，发现本研究需要补4个缺失的研究，而且该4个研究分布在无统计学意义区域（白色区域），提示该Meta分析可能存在发表偏倚。

参考资料：

1.http://www.jebm.cn/article/2013/1671-5144-13-5-307.html

阅读: 910