R 绘制Kaplan-Meier生存曲线

Kaplan-Meier (KM) 是一种非参数估计的方法用以描述观测变量的生存随时间变化的一个概率分布（Kaplan and Meier, 1958）：

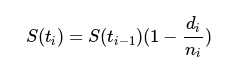
t_i 表示第 i 个时间点（t₀=0，S(0) = 1）
n_i 表示在 t_i 之前的有效人数
d_i 表示在 t_i 死亡的人数
S(t_i-1) 表示在上一个时间点 i-1 的生存概率

通常用survival计算生存概率，用survminer可视化展示，首先安装：

# 可以采用国内源
install.packages(c("survival", "survminer"))

用包自带的肺癌的数据做后续的演示：

library(survival)
library(survminer)
library(ggthemes)

# 加载演示数据
data("lung")
# 计算年龄和生存之间的关系
fit <- survfit(Surv(time, status) ~ sex, data = lung)
# 绘制生存曲线
ggsurvplot(
  fit,
  pval = TRUE,
  conf.int = TRUE,
  # 添加生存表格
  risk.table = TRUE,
  # 改变生存表的颜色
  risk.table.col = "strata",
  # 线的类型
  linetype = "strata",
  # 添加median值虚线
  surv.median.line = "hv",
  # ggplot2主题
  ggtheme = theme_few(),
  palette = c("red", "blue")
)

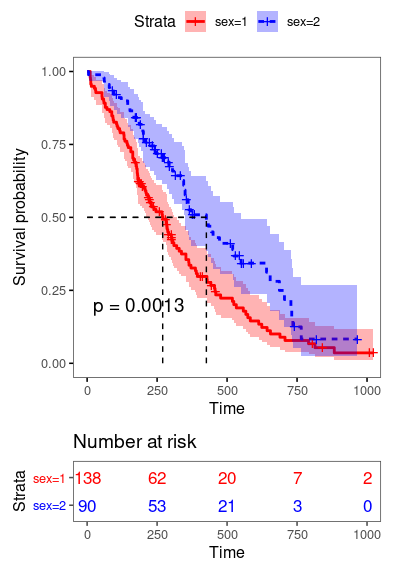
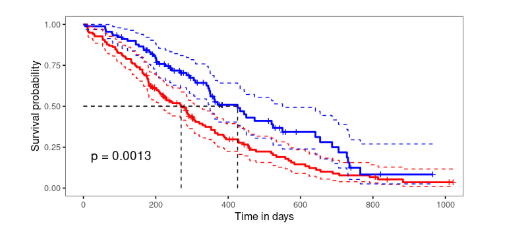
定制你的生存曲线：

ggsurvplot(
  fit,
  # 显示P值
  pval = TRUE,
  # 是否显示置信区间
  conf.int = TRUE,
  conf.int.style = "step",
  xlab = "Time in days",
  # 时间刻度
  break.time.by = 200,
  ggtheme = theme_few(),
  # 风险表相关
  risk.table = "abs_pct",
  risk.table.y.text.col = T,
  risk.table.y.text = FALSE,
  # 添加对应时间的观测频数
  ncensor.plot = TRUE,
  surv.median.line = "hv",
  legend.labs =
    c("Male", "Female"),
  palette =
    c("red", "blue")
)

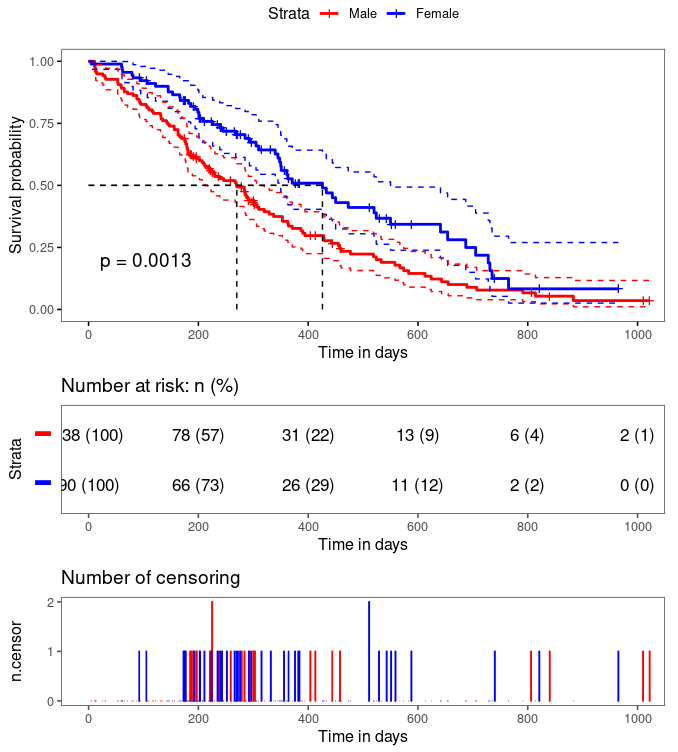
同时也可以用事件累计发生率来描述生存状态：

ggsurvplot(
  fit,
  conf.int = TRUE,
  risk.table.col = "strata",
  ggtheme = theme_few(),
  palette = c("red", "blue"),
  # 修改此处的fun参数即可
  fun = "event"
)

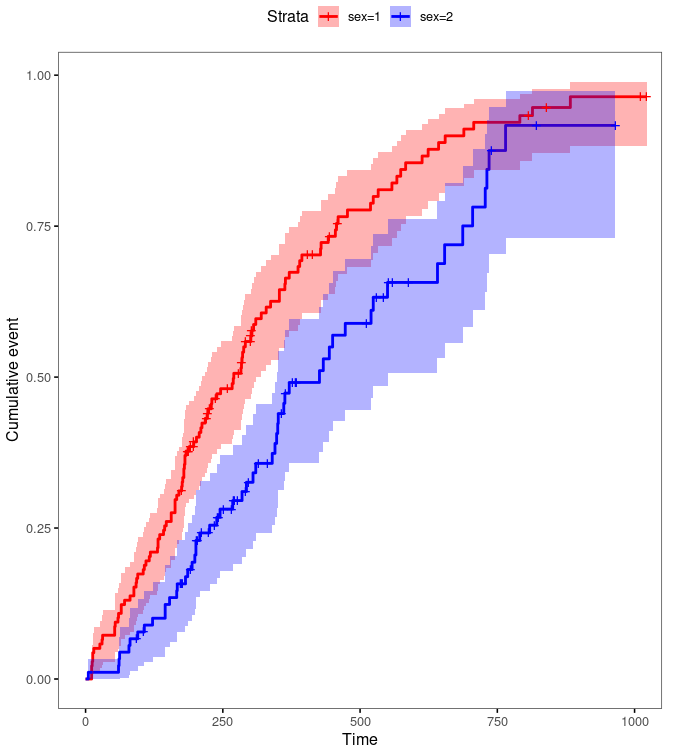
生存分析常常用来研究事物的发展规律，比如研究某种药物的疗效、手术后的存活时间等。

参考资料：

1.https://www.r-bloggers.com/survival-analysis-basics/