ANOVA（Analysis of variance）简称方差分析或者“变异系数分析”，用于两个及两个以上样本均数差别的显著性检验。主要用于检验两个或多个样本均数间的差异有无统计学意义或者检验两个或多个因素间有无相互作用。

常见的方差分析：

  • one-way ANOVA（单因素ANOVA分析）
  • two-way ANOVA（双因素ANOVA分析）
  • N-way ANOVA（多因素方差分析）

方差分析主要假设（前提，特殊假设有其他ANOVA方法）：

  • 方差齐性
  • 符合正态分布
  • 组间相互独立的

下面用R一步步演示ANOVA分析，如下：

演示数据：data下载

# 安装要用到的安装包 install.packages(c("ggplot2", "ggpubr", "tidyverse", "broom", "AICcmodavg", "gplots"))

library(ggplot2)
library(gplots)
library(ggpubr)
library(tidyverse)
library(broom)
library(AICcmodavg)

# 加载数据
data <-
  read.csv(
    "data.csv",
    header = TRUE,
    colClasses = c("factor", "factor", "factor", "numeric")
  )

summary(data)

# 检查数据是否符合假设
hist(data$yield)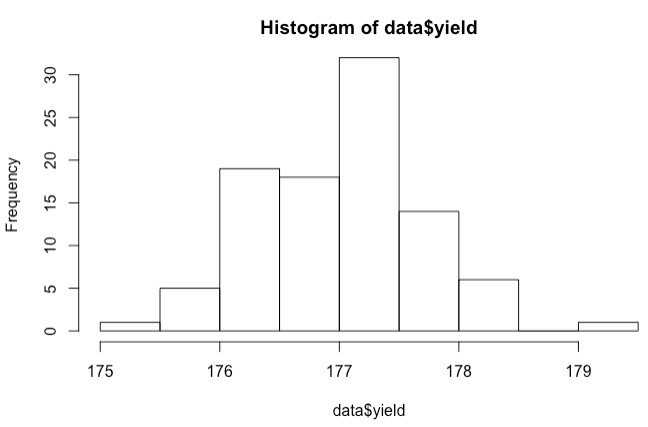

# 单因素ANOVA
one.way <- aov(yield ~ fertilizer, data = data)
summary(one.way)

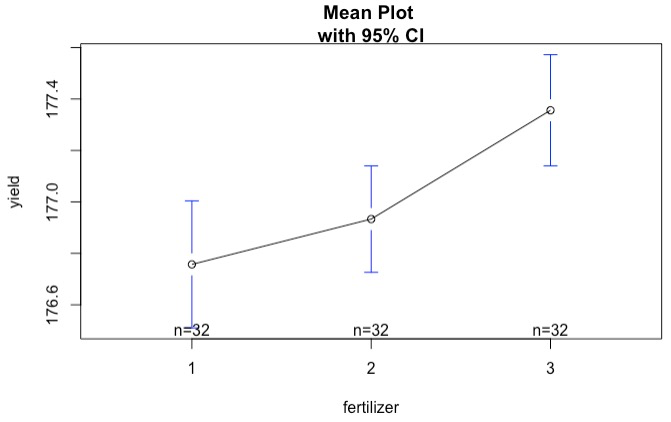
结果说明fertilizer的使用对yield影响很显著（p < 0.001）


#  双因素ANOVA
two.way <- aov(yield ~ fertilizer + density, data = data)
summary(two.way)

说明fertilizer和的density对yield影响都很显著（p < 0.001）

接下来比较两种模型方法那种更合适，我们利用AICcmodavg包来评估AIC打分：


# 比较不同分析模型
model.set <- list(one.way, two.way)
model.names <- c("one.way", "two.way")

aictab(model.set, modnames = model.names)

一般AIC（赤池信息量 akaike information criterion，是衡量统计模型拟合优良性的一种标准，AIC越小，模型越好，通常选择AIC最小的模型）得分最低的模型，说明two-way ANOVA分析最适合该数据。

模型查看：


par(mfrow=c(2,2))
plot(two.way)
par(mfrow=c(1,1))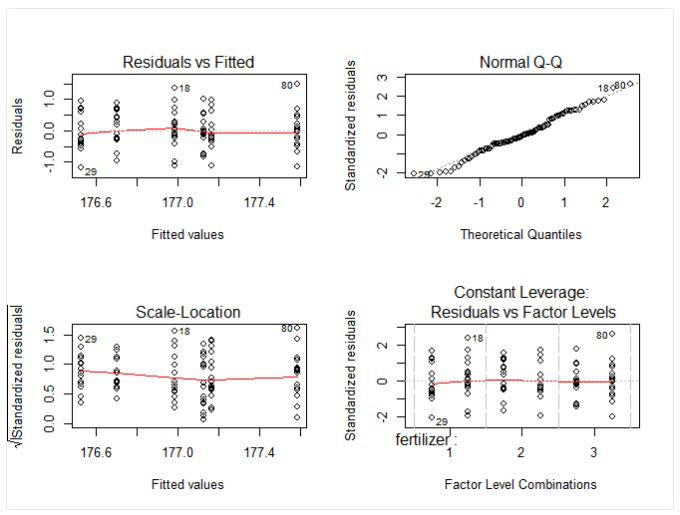

模型检验（HSD检验法，任何一对平均值之差只要超过HSD值，就表明这一对平均值之间的差别是显著的）：


# 模型验证
tukey.two.way<-TukeyHSD(two.way)
tukey.two.way

结果发现fertilizer3和1之间以及fertilizer3和2之间存在显着差异（p <0.05），但是fertilizer2和1之间没有显着差异；density2和1之间也存在显著差异（p < 0.001）。

参考资料：

1.https://www.scribbr.com/statistics/anova-in-r/

2.http://onlinestatbook.com/2/analysis_of_variance/one-way.html

阅读: 890