t-SNE 全称 T 分布随机近邻嵌入（T-Distribution Stochastic Neighbour Embedding）是一种用于降维的机器学习方法，它能帮我们识别相关联的模式。t-SNE 主要的优势就是保持局部结构的能力。这意味着高维数据空间中距离相近的点投影到低维中仍然相近。

t-SNE 同样能生成漂亮的可视化。下面介绍使用R语言实现t-SNE的过程。

本文介绍使用R包：Rtsne

Rtsne是一个专门进行t-SNE降维分析的R包，安装方式如下：

install.packages("Rtsne") # Install Rtsne package from CRAN

或者从github直接安装使用

if(!require(devtools)) install.packages("devtools") # If not already installed
devtools::install_github("jkrijthe/Rtsne")

安装好Rtsne后我们可以用iris的公共数据集来测试下t-SNE

step1.首先我们查看下iris数据集的格式：

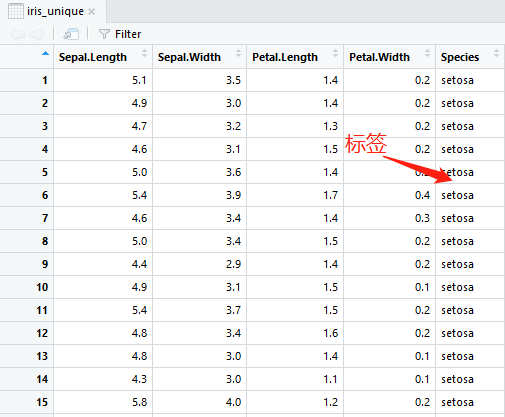
step2.使用Rtsne包进行降维

library(Rtsne)
iris_unique <- unique(iris) # Remove duplicates
set.seed(42) # Sets seed for reproducibility
tsne_out <- Rtsne(as.matrix(iris_unique[,1:4])) # Run TSNE

step3.绘图

plot(tsne_out$Y,col=iris_unique$Species,asp=1) # Plot the result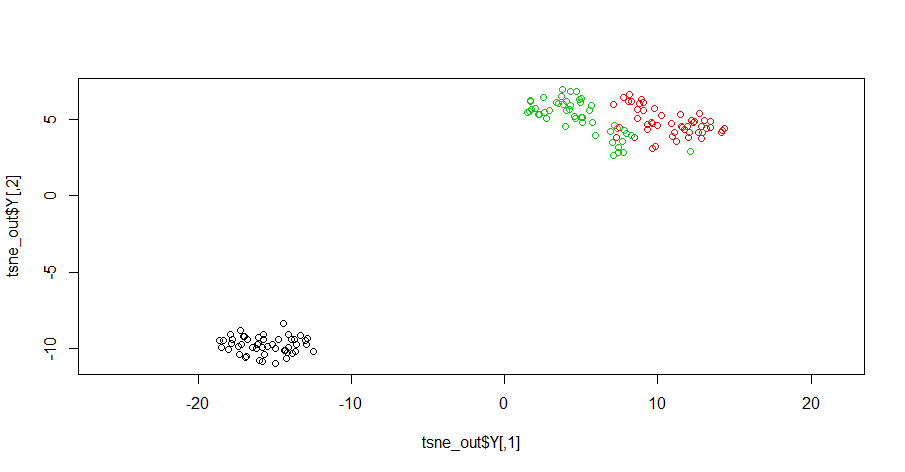

写在后面的话

Rtsne函数（主要参数介绍）：

Rtsne(X, dims = 2, initial_dims = 50,
  perplexity = 30, theta = 0.5, check_duplicates = TRUE,
  pca = TRUE, partial_pca = FALSE, max_iter = 1000,
  verbose = getOption("verbose", FALSE), is_distance = FALSE,
  Y_init = NULL, pca_center = TRUE, pca_scale = FALSE,
  normalize = TRUE, stop_lying_iter = ifelse(is.null(Y_init), 250L,
  0L), mom_switch_iter = ifelse(is.null(Y_init), 250L, 0L),
  momentum = 0.5, final_momentum = 0.8, eta = 200,
  exaggeration_factor = 12, num_threads = 1, ...)

dims参数设置降维之后的维度，默认值为2；

perplexity参数的取值必须小于(nrow(data) – 1 )/ 3;

theta参数取值越大，结果的准确度越低，默认值为0.5；

max_iter参数设置最大迭代次数；

pca参数表示是否对输入的原始数据进行PCA分析，然后使用PCA得到的topN主成分进行后续分析，t-SNE算法的计算量是特别大的，对于维度较高的数据数据，先采用PCA降维可以有效提高运行的效率，默认采用top50的主成分进行后续分析，当然也可以通过initial_dims参数修改这个值。

最后分享一个来自网络的t-SNE降维的动图，加深大家的理解。

下载区：

Rtsne帮助文件下载

参考资料：

1. 论文http://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf

2.https://cran.r-project.org/web/packages/Rtsne/Rtsne.pdf

3.https://cran.r-project.org/web/packages/Rtsne/index.htm

4.https://blog.csdn.net/scott198510/article/details/76099700

5. L.J.P. van der Maaten and G.E. Hinton. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9(Nov):2579-2605, 2008.

6. L.J.P. van der Maaten. Barnes-Hut-SNE. In Proceedings of the International Conference on Learning Representations, 2013.

阅读: 2,711