t检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著，在数据分析中我们常用T-Test来估算两组数据是否有显著的差异，此处不在赘述t检验基本原理，本文主要介绍几种不同形式的t检验方法。

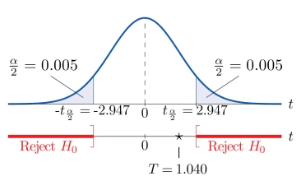
t检验适用的条件：

  1. 已知一个总体均数
  2. 可得到一个样本均数及该样本标准差
  3. 样本来自正态或近似正态总体

在R语言中，t-test的函数为t.test()，下面简单介绍其参数：


# ?t.test查看帮助信息
t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

x，y ：为进行检验的数据
alternative：该参数设置假设是单尾还是双尾，默认为双尾检验。
mu：单样本检验时，需要设定的平均值
paired：是否进行配对t-test。
var.equal：方差是否相等
conf.level：显著性水平，默认α=0.05

t检验主要分为以下几种类型：

  1. 单样本 t-tests（ one-sample t-tests ）
  2. 非配对t检验或独立t检验（ unpaired t-test or independent t-test ）：
    • Student’s t-test（方差齐）
    • Welch’s t-test （方差不齐）
  3. 配对t检验（ paired t-test ）

1） 单样本 t-tests

单样本t检验，也称为单参数t检验或单样本t检验，用于比较一个样本的均值与一个已知的标准(或理论/假设)均值。

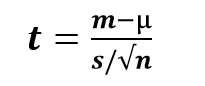
m = 样本均值
µ = 理论值或总体均值
s = 样本的的标准差
n = 样本大小

分析步骤：

  • 导入数据
  • Q-Q plot查看是否满足正态分布
  • t检验

2） 非配对t检验

非配对t检验用于比较两个独立组，非配对t检验又分为方差齐（ Student’s t-test ）和方差不齐（ Welch’s t-test ），这两种方法一般来说有着非常相似的结果，除非两组的数量和标准差有很大的不同。

  • Student’s t-test：var.equal = TRUE
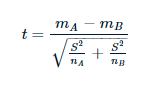
  1. mA 、 mB 是两组的平均值
  2. nA 、 nB 是两组的样本数量
  3. S2 是两个样本共同方差的估计量
  • Welch’s t-test：var.equal = FALSE
  1. SA 和 SB 分别是A组和B组的标准差

Welch’s t-test的自由度估计如下

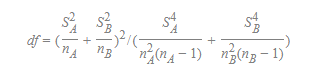
分析步骤：

  • 导入数据
  • Q-Q plot查看是否满足正态分布
  • 检查方差齐性
  • 方差齐用 Student’s t-test ，方差不齐用 Welch’s t-test

3） 配对t检验

配对t检验要求两个样本间必须成对，每一对样本除随机地给予不同处理外，其他实验条件应尽量一致，两样本的容量必定相等。

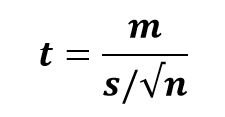
m = 样本的平均值
µ = 理论值或总体均值
s = 样本的标准差
n = 样本大小

R 中，t.test 中paired = TRUE即可。

本次介绍到此，大家可以根据不同的实验设计、或者数据性质选择合适的方法。

参考资料：

1.https://www.analyticsvidhya.com/blog/2019/05/statistics-t-test-introduction-r-implementation/

2.https://www.datanovia.com/en/lessons/types-of-t-test/

阅读: 10,614