1927年，美国数学家 Edwin Bidwell Wilson提出了一个修正公式，被称为”威尔逊置信区间”，也称为“Plus Four Confidence Intervals”，假定用于估计的统计样本具有二项式分布：

  • 将实验重复固定次数；
  • 实验有两个可能的结果（“成功”和“失败”）；
  • 每个实验的成功概率相等；
  • 试验在统计上是独立的

其在小样本量的情况下表现也很好，因为该方法考虑了这些情况下的不确定性。

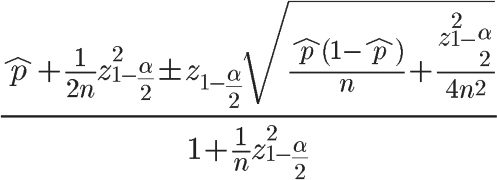
很多医学统计文章中使用 Wilson confidence intervals来计算置信区间，类似的计算如：R语言使用binom.test函数、Hmisc包binconf函数、fastR2的wilson.ci函数或者使用python的scipy也可以计算。

下面用python从公式做演示计算 Wilson confidence intervals。

一个示例，如下：

Abbreviations: NIFTP, Noninvasive
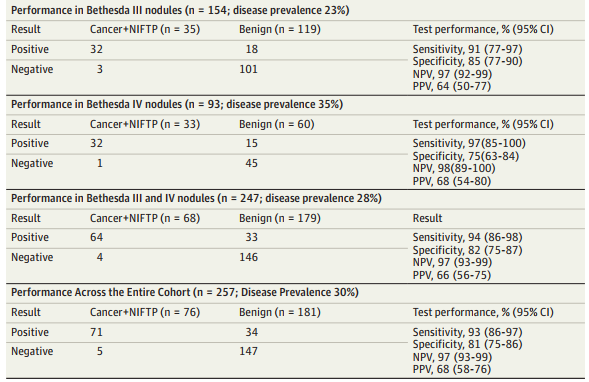
follicular thyroid neoplasm with
papillary-like nuclear features;
NPV, negative predictive value;
PPV, positive predictive value.

以置信区间 𝐶𝐿 = 0.95， 我们知道 𝛼= 1 – 0.95 = 0.05 ，有α/2=0.025，查表得到z=1.96

 置信区间Z值
80%1.282
85%1.440
90%1.645
95%1.960
99%2.576
99.5%2.807
99.9%3.291

代码实现如下：

#!/usr/bin/python
#coding=utf8

import numpy as np

def wilson_CI(nd, n, z=1.96):
    """
    威尔逊置信区间计算函数
    :param nd: 正例数
    :param n: 总数
    :param z: 正太分布的分位数（查表0.95的置信区间约等于1.96）
    :return: 威尔逊置信区间
    """
    p = nd * 1. / n * 1.
    low = (p + (np.square(z) / (2. * n))
             - ((z / (2. * n)) * np.sqrt(4. * n * (1. - p) * p + np.square(z)))) / (1. + np.square(z) / n)

    high = (p + (np.square(z) / (2. * n))
             + ((z / (2. * n)) * np.sqrt(4. * n * (1. - p) * p + np.square(z)))) / (1. + np.square(z) / n)
    return (low, high)


if __name__ == "__main__":
    z = wilson_CI(45,49)
    print(z)

上述代码可以得到上述文章类似结果。

参考文章：

1.https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binom_test.html

2. https://en.wikipedia.org/wiki/Binomial_test

3.https://www.itl.nist.gov/div898/handbook/prc/section2/prc241.htm

4.http://jamanetwork.com/journals/jamaoncology/fullarticle/2713846

5.https://blog.csdn.net/andy_shenzl/article/details/81453509

6.http://www.evanmiller.org/ranking-items-with-star-ratings.html#examples

7.https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval

阅读: 4,689